電磁気学の気持ち

2025/3/3

そもそも、電気と磁気とは何か？

電磁気学は、電気と磁気の性質について追求する分野です。ただ、この二つの言葉は日常的に使われていて多義語すぎるため、より厳密な表現として 「電荷」と「電場」、「電流」と「磁場」 が使われます。

そして、「電荷」と「電場」、「電流」と「磁場」が引き起こす現象を 電気的・磁気的な現象 という風に総称することが多いです。

また、電気的な現象 と 磁気的な現象 は密接に関連していて、完全に区別することは困難です。

そこで、「電荷」と「電場」、「電流」と「磁場」 について、その定義と性質、関係性を見て、電磁気学を理解していきましょう。

少し長いですが、これら 4 つの概念を理解すれば、電磁気学の基礎は理解できたと言っても過言ではありません。

電荷とは

電荷とは、直感的には「物体が持つ電気」です。電荷の単位は「クーロン(C)」であり、正負両方を取ります。「電気」と言われて持つイメージに一番近いのが、この電荷でしょう。

微視的に見ると、電子が $-1.6 \times 10^{-19}$ C の負電荷、陽子が $1.6 \times 10^{-19}$ C の正電荷を持っており、物体内の電子と陽子の数の差によって、その物体の電荷が決まります。

電荷を持つ物体自体のことを、電荷と呼ぶこともあります。

電荷は、同符号同士のものは反発し、異符号同士のものは引き合う という性質を持っています。

そのため、電荷を持つ物体は互いに力を及ぼし合う と考えることができるのですが、電磁気学では、あまりそう考えることはありません。 その代わりとして、「電場」 を導入して、電荷が電場によって力を受けるという考え方を取ります。

前者の考え方は遠隔作用、後者の考え方は近接作用と呼ばれます。例えば万有引力は遠隔作用の考え方と言えるでしょう。

そこで次は、電場について見ていきましょう。

電場とは

電場とは、直感的には電荷によるオーラです。 空間に、どのくらい電荷の影響があるか を表す量とも言えるでしょう。

空間中のどの位置にも、電場が定義されます。 温度などと同じですね。（図はこちらより引用）

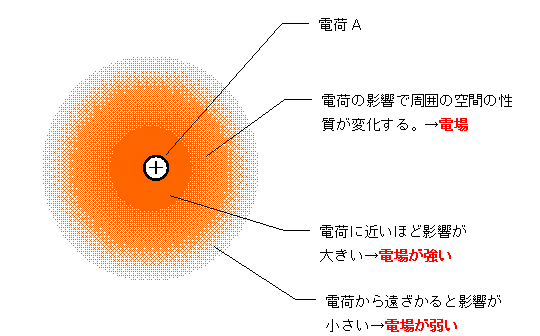
ただ、温度とは異なり、電場は 大きさと向きと持つベクトル量 です。そのため、この位置には向き〇〇、大きさ ×× の電場が存在している、というように表現します。
（ここにはこっち向きにこれくらいのオーラあるわ〜、というイメージでしょうか）

電場の向きは、電荷が正なら電荷から離れる向き、負なら電荷に向かう向きとなり、電荷に近いほど電場の大きさは大きくなります。

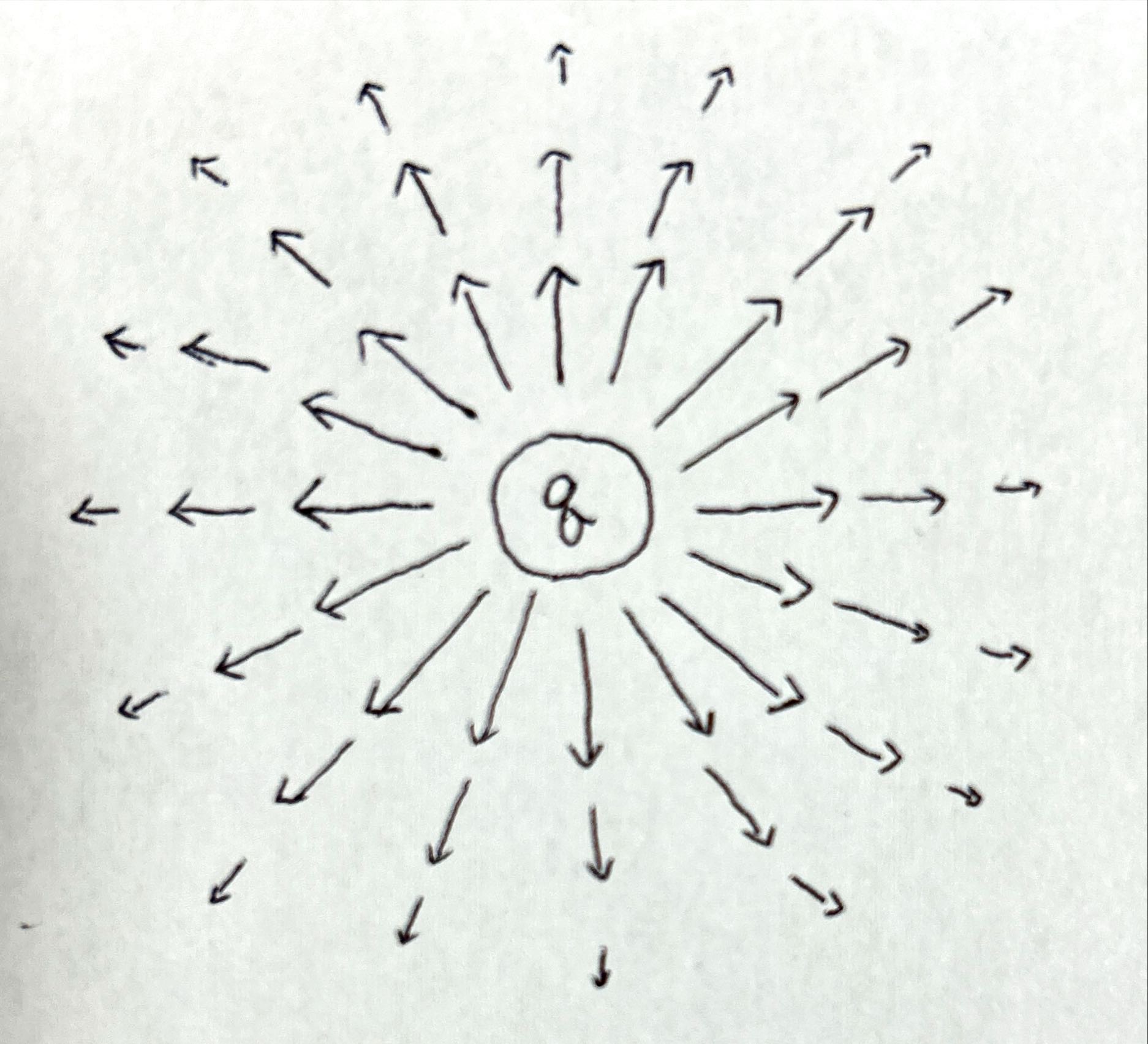
式にすると以下の通りですが、上記のイメージを持てればひとまず大丈夫でしょう。

電場

電荷 $q$ が位置 $\bm{r}_0$ にあるとき、位置 $\bm{r}$ における真空中の電場 $\bm{E}$ は、以下のように表される。

\bm{E}(\bm{r}) = \frac{1}{4\pi\varepsilon_0} \frac{q}{|\bm{r} - \bm{r}_0|^2} \frac{\bm{r} - \bm{r}_0}{|\bm{r} - \bm{r}_0|}

$k_0 = \frac{1}{4\pi\varepsilon_0}$ であり、向きを考えなければ、 $E = k_0\frac{q}{(r - r_0)^2}$ とお馴染みの式になります。

また、複数の電荷があれば、電場を重ね合わせたものがその位置での電場となります。オーラが重なっているイメージですね。

電荷が受ける力と電場の関係

そして、電荷を持つ物体は電場によって力を受けます。

イメージとしては、その空間に電場オーラがあると、電荷を持つ物体はオーラの影響を受けて力が働く、という感じでしょうか。

クーロンの法則 とも呼ばれるものです。また、電荷が受ける力を クーロン力 と呼びます。

その力は、その位置の電場 $\bm{E}$ 、置いた物体の電荷 $q$ とすると、 $\bm{F} = q\bm{E}$ となります。

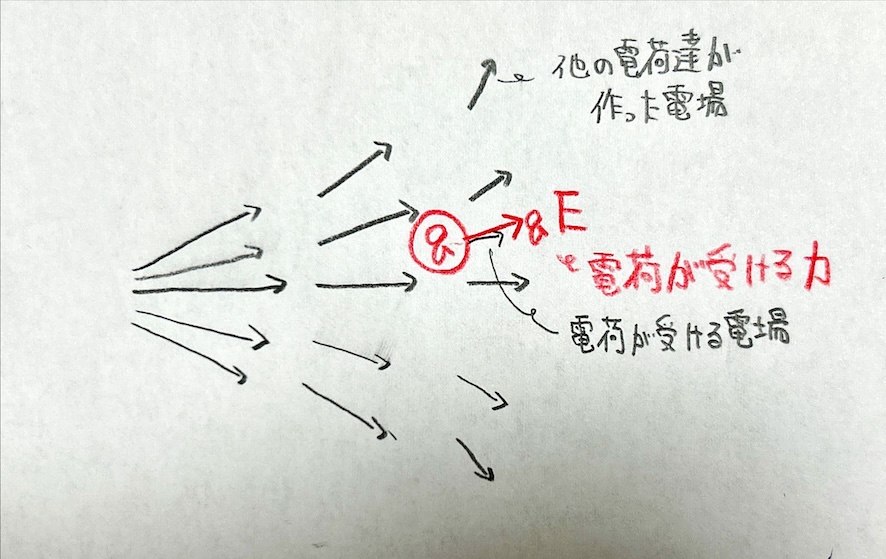
ここまで数式が少し多くなってしまったので、言葉でまとめると、電荷が存在することによって、その空間に電場が生じ、他の電荷はその電場によって力を受ける というわけです。

感覚的にまとめるとしたら、各物体は固有の "電気" を持っていて、それにより周囲に "電気的なオーラ" が生じ、そのオーラによって他の物体は、自分が持つ "電気" に応じた影響を受ける、という感じでしょうか。

電流とは

電流とは、直感的には「電気の流れ」ですが、少し注意が必要です。

微視的に見ると、電子が移動する ことによって電流が生じます。（陽子は基本的に動きません）

電流の向きと電子の移動の向きは、ややこしいことに逆向きです。

一番身近なのは、導線や金属などで電子が移動することによって生じる電流でしょう。ただし、それだけではありません。

例えば磁石では、磁石の中の電子がとても小さいループを作って "動いている" ことによって "電流" が生じています。（正確には、電子のスピンです）

他にも、物体内部の電子の分布が変わる時にも電流が生じます。

つまり、電子の移動によって電流が生じるのですが、導線を流れるようなわかりやすいものだけでなく、様々な場所で電流は生じる というわけです。

磁場とは

磁場とは、直感的には電流によるオーラです。 空間に、どのくらい電流の影響があるか を表す量とも言えるでしょう。

電場と同様に、空間中のどの位置にも磁場が定義され、大きさと向きと持つベクトル量 となります。

つまり、電荷が存在すれば電場が存在するし、その電荷が動いていれば磁場も存在する、というわけです。

電場と磁場の区別がわからなくなった皆さん、安心してください。電場と磁場は完全には区別できません！（この部分は相対論も絡んでいて難しいです……）

磁場の向きは、右ネジの法則 に従い、電流に近いほど磁場の大きさは大きくなります。（右ネジの法則 は単に磁場の向きを決めているだけなので、興味があれば調べてみてください）

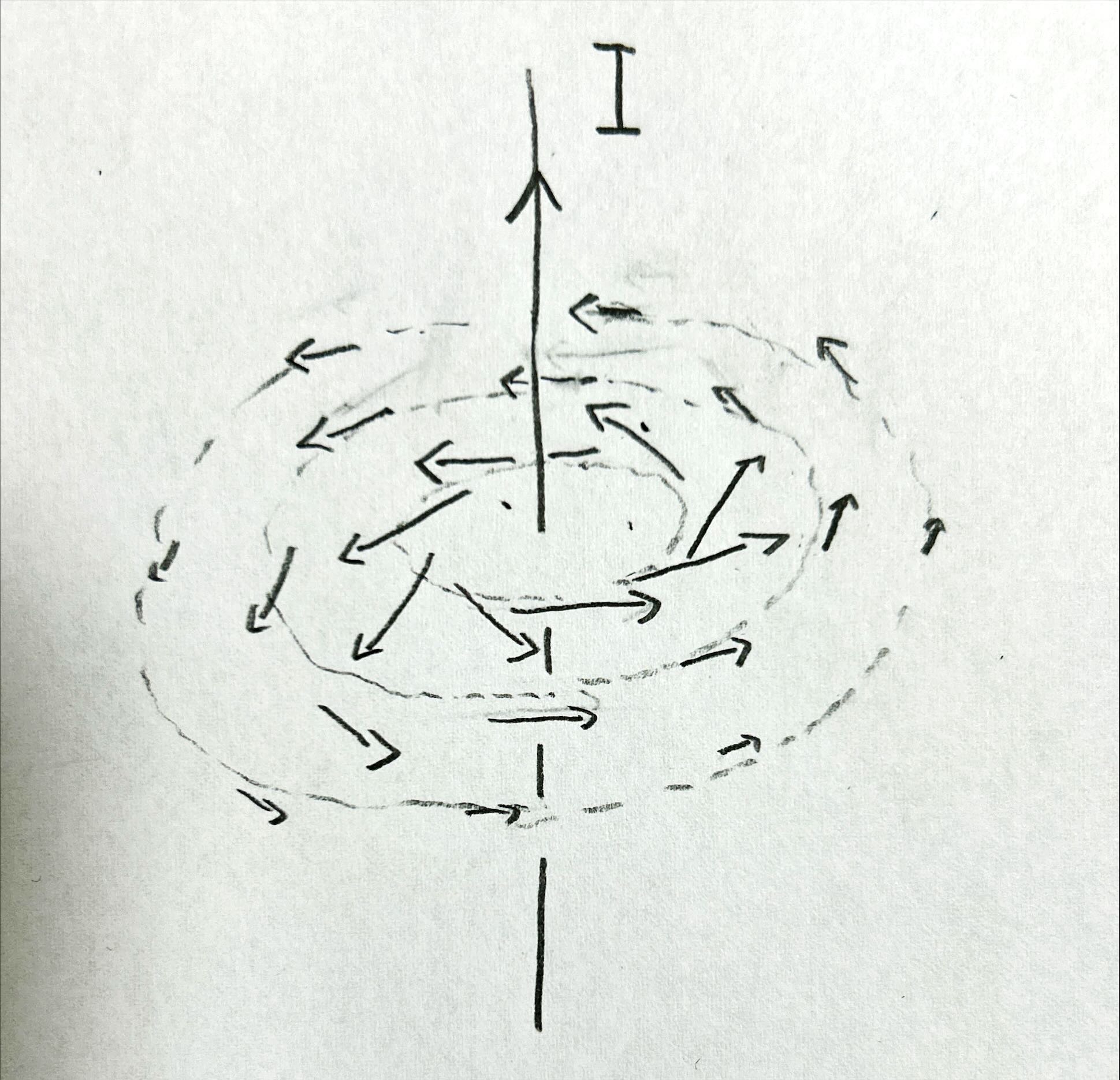
式にすると以下の通りですが、同様にイメージを持てればひとまず大丈夫でしょう。

磁場

電流 $I$ が位置 $\bm{r}_0$ の微小区間 $d\bm{l}$ に流れているとき、その電流素片による位置 $\bm{r}$ における真空中の磁場 $d\bm{B}$ は、以下のように表される。

d\bm{B}(\bm{r}) = \frac{\mu_0}{4\pi} \frac{Id\bm{l} \times (\bm{r} - \bm{r}_0)}{|\bm{r} - \bm{r}_0|^3}

この法則は、ビオ・サバールの法則 と呼ばれており、実際にはこの式を積分するなどして磁場を求めます。

有名な、円形電流による磁場 $B = \frac{\mu_0 I}{2r}$ や直線電流による磁場 $B = \frac{\mu_0 I}{2\pi r}$ もこの法則から求められます。

ここで重要なのは、磁場は電流によって生じるものである ということです。

昔は、例えば磁石は磁荷があることによって磁場が生じると考えられていましたが、現在では、磁荷は存在せず、磁石内部の電流（正確には電子のスピン）によって生じるとわかっています。

電流が受ける力と磁場の関係

そして、電荷と同様に、電流を持つ物体は磁場によって力を受けます。

イメージは、その空間に磁場オーラがあると、電流を持つ物体はオーラの影響を受けて力が働く、という感じでしょうか。電荷と電場の関係性と全く同じですね。

いわゆる、フレミングの左手の法則 です。また、電流が受ける力を アンペール力 と呼びます。

その（単位長さあたりの）力は、その位置の磁場 $\bm{B}$ 、流れる電流 $\bm{I}$ とすると、 $\bm{F} = \bm{I} \times \bm{B}$ となります。

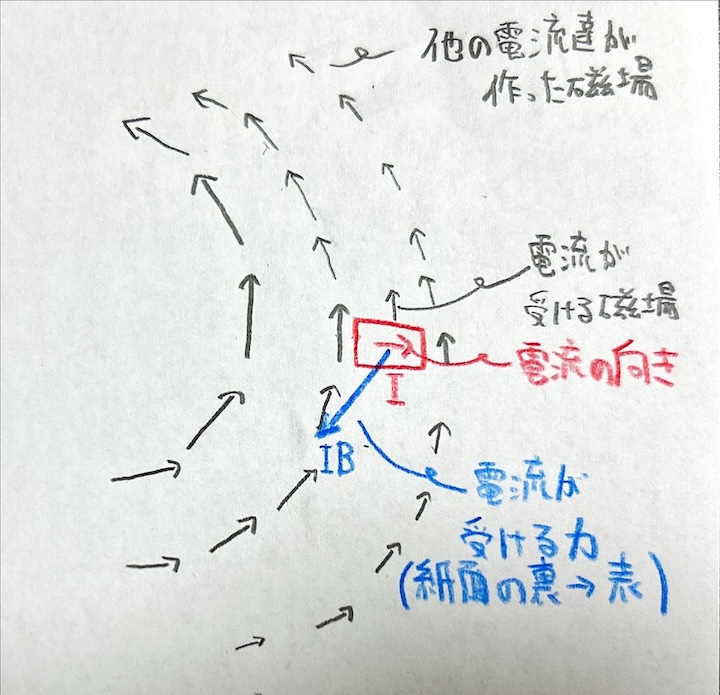
つまり、これまでの電流と磁場の関係性を言葉でまとめると、電流が存在することによって、その空間に磁場が生じ、他の電流はその磁場によって力を受ける というわけです。

大丈夫でしょうか？ここまで、電荷と電場、電流と磁場 についてその関係性を見てきました。

ここまでをまとめておきましょう。

電荷は物体が持つ電気で、物体内の電子と陽子の数の差によって決まる。
電場は電荷によるオーラで、空間中のどの位置にも定義される。
電荷は電場によって力を受ける。（クーロンの法則により計算でき、クーロン力と呼ばれる）
電流は電気の流れで、電子の移動によって生じる。
磁場は電流によるオーラで、空間中のどの位置にも定義される。
電流は磁場によって力を受ける。（フレミングの左手の法則により計算でき、アンペール力と呼ばれる）

電磁気学の実用例

ここまでで、電磁気学を考える上で必須の 「電荷」「電場」「電流」「磁場」 についてある程度理解できたと思います。より厳密な関係性や数式については、別の記事に書いているので、もし興味があれば、そちらも読んでみてください。

マクスウェルの方程式の気持ち【電磁気学】

マクスウェルの方程式は、電磁気学の基本となる方程式です。複雑な式にも思える、マクスウェルの方程式の本質をわかりやすく論理的に解説します。

電磁気学は、この 「電荷」「電場」「電流」「磁場」 の概念を基本として、様々な現象を説明し、社会に応用されています。

ここでは、その応用例をいくつか紹介しましょう。直感的には、 電気に関わるもの はすべて電磁気学をもとにしています。また、電気を主として実装することが多いですが、中には、磁気的な現象を利用するものもあります。

電子機器：テレビ、パソコン、スマホ、電子レンジ……。世の中の電子機器は全て電磁気学の応用です。例えば、抵抗は、電場と電流の関係性を定義し、コイルは、電流と磁場の関係性、コンデンサは電荷と電場の関係性を利用しています。
モーターや発電機：電気を使って動力を得る場合に使われます。電気自動車もその一つですね。電流と磁場の関係性を利用することが多いです。
電波・光：実は、通信で使われている電波も電磁気学の応用です。光自体も、電磁波の一種で電磁気学の一分野として扱われます。ここで着目されているのは、電場と磁場の関係性です。
磁気記録：磁気的な性質はデータの記録にも使われており、ハードディスクや磁気カードなどに使われています。