マクスウェルの方程式の気持ち【電磁気学】

物理の記事 でも説明したように、物理は、自然界の現象をできるだけ単純な法則・数式で説明するためのものです。

物理とは何なのか？

そもそも、物理学とは何なのでしょうか？物理を学ぶ際には必ず知っていてほしい、物理学の基本的な考え方と実用例について解説します。

その中でも マクスウェルの方程式 は、電気 と 磁気 の性質を説明するための方程式であり、運動方程式と並んで最重要な方程式の一つです。

具体的には、電荷、電場、電流、磁場 の関係性を数式で表現する方程式となります。

この記事では、複雑なマクスウェルの方程式の本質を、なるべくわかりやすくかつ論理的に解説します。

電磁気学のそもそも

電磁気学については、こちら の記事で詳しく解説しているので、 電磁気学の概要について知りたい場合は、そちらを先に読んでみてください。

電磁気学の気持ち

電磁気学とはどのような分野なのか？電磁気学の本質と実用例をわかりやすく解説します。

ここでは、その中でも大事なことを抽出します。

ここまでが、電磁気学を考える上で必須の 「電荷」「電場」「電流」「磁場」 についての簡単な定義と関係性です。

しかし、実はこの式は、電荷や電流が時間変化しない場合の式 にあたります。実際の世界では、電荷や電流は時間変化することが多いので、それを考慮したいです。

• 時間変化しないのは、電気回路で電流一定の場合などでしょうか。

そこで、これらの関係性にプラスして、電荷と電流の 時間変化 を考えて、 「電荷」「電場」「電流」「磁場」についての関係性を数式でまとめたもの が、マクスウェルの方程式 になっています。

ただ、まずはこれまでの 時間変化がない場合の関係性 を整理する必要があるので、そこから始めましょう。

---

電荷と電場の関係

まず、電荷と電場の関係性を整理します。 端的には、以下の数式が成り立つということでした。

$$\bm{E}(\bm{r}) = \frac{1}{4\pi\varepsilon_0} \frac{q}{|\bm{r} - \bm{r}_0|^2} \frac{\bm{r} - \bm{r}_0}{|\bm{r} - \bm{r}_0|}$$

$\bm{E}(\bm{r})$ が電場、$q$ が電荷でしたね。 しかし、この式は 1 つの電荷 による電場しか表していません。そこで、空間中の全電荷を考慮した式 を作成しましょう。

ここで、位置 $\bm{r}$ における 電荷密度 $\rho(\bm{r})$ を導入します。質量を考えるときに密度を導入したように、電荷も電荷密度というものを考えるわけです。

例えば、電荷密度 $1~\text{C/m}^3$ の空間が $1~\text{m}^3$ あると、その空間には $1~\text{C}$ の電荷が含まれています。 質量と密度の関係と全く同じです。

そして、これを数式で表すと $\displaystyle q = \int \rho(\bm{r}) dV$ となります。 積分が出てきてややこしいですが、空間の電荷密度を足し合わせると、電荷になる ということを表すだけの式です。
例えば質量も、密度を $\rho(\bm{r})$ とすれば、$\displaystyle m = \int \rho(\bm{r}) dV$ と表されます。

さて、電荷と電場の関係式を、これを用いて書き直しましょう。すると、以下のようになります。

$$\bm{E}(\bm{r}) = \frac{1}{4\pi\varepsilon_0} \int \frac{\rho(\bm{r}_0)}{|\bm{r} - \bm{r}_0|^2} \frac{\bm{r} - \bm{r}_0}{|\bm{r} - \bm{r}_0|} dV_0$$

イメージとしては、ある位置 $\bm{r_0}$ にある電荷による電場を、積分によって全ての位置にわたって足し合わせている、という感じでしょうか。

これが、一般的な 電場と電荷が満たす関係式 となります。（これ自体をクーロンの法則と呼ぶこともあります）

ガウスの法則

ただ、この式と等価な式として使われるものがもう一つあります。それが、下記の二つの数式です。特に、一つ目の式は ガウスの法則 と呼ばれています。

$$\begin{align} & \nabla \cdot \bm{E} = \frac{\rho(\bm{r})}{\varepsilon_0}\\ & \nabla \times \bm{E} = \bm{0} \end{align}$$

なぜ、この二つの数式を合わせると先程の式と等価になるのかは、式変形が複雑なため省きますが、それぞれの式のイメージは以下の通りです。

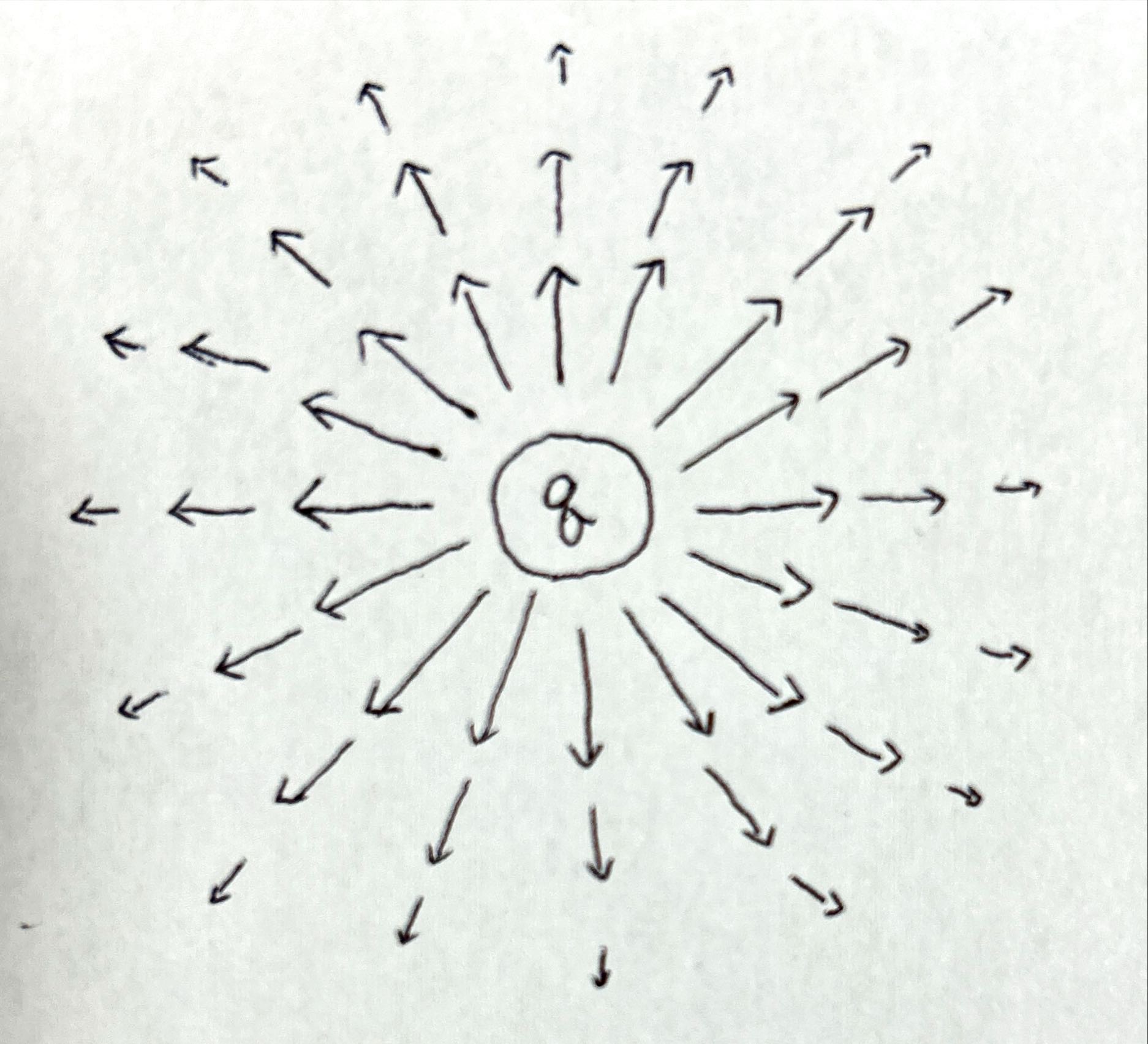
• $(1)$ ガウスの法則：電荷の値に応じて、どのように電場が電荷を中心に広がっているかを表します。 $\nabla \cdot \bm{E}$ は、$\text{div} \bm{E}$ とも書かれ、発散 を表します。
• $(2)$：電場の広がり方を規定し、ここでは、直感的には 渦状にはならないこと を表します。 $\nabla \times \bm{E}$ は、$\text{rot} \bm{E}$ とも書かれ、回転 を表します。

これらの式を合わせれば、「電場は電荷の大きさに応じて、電荷から放射状に広がってるよね」 ということを表せるというわけです。

今の所、難しい上に恩恵がないため、このような式変形の嬉しさはわからないですが、後々、マクスウェルの方程式を作成する際に重要になってきます。

• 電磁気学が難しいと言われる所以は、このようなベクトル解析を使った微積分が多いことによります。 そのため、特に初学者であれば、数式を理解することよりもその背後の物理的なイメージを持つことの方が重要かもしれません。

---

電流と磁場の関係

次に、電流と磁場の関係性を整理します。 端的には、以下の数式が成り立つということでした。

$$d\bm{B}(\bm{r}) = \frac{\mu_0}{4\pi} \frac{Id\bm{l} \times (\bm{r} - \bm{r}_0)}{|\bm{r} - \bm{r}_0|^3}$$

$\bm{B}(\bm{r})$ が磁場、$I$ が電流でしたね。 しかし、この式も 微小な区間の電流 による磁場しか表していません。そこで、空間中の全電流を考慮した式 を作成しましょう。

同様に、位置 $\bm{r}$ における 電流密度 $\bm{i}(\bm{r})$ を導入し、式を変形すれば、以下のようになります。

$$\bm{B}(\bm{r}) = \frac{\mu_0}{4\pi} \int \frac{\bm{i}(\bm{r}_0) \times (\bm{r} - \bm{r}_0)}{|\bm{r} - \bm{r}_0|^3} dV_0$$

これが、一般的な 磁場と電流が満たす関係式 となります。（これ自体をビオ・サバールの法則と呼ぶこともあります）

さらに磁場についても、発散 $\nabla \cdot \bm{B}$ の式と、回転 $\nabla \times \bm{B}$ の式を考えていくと、以下のようになります。 一つ目の式は ガウスの法則、二つ目の式は アンペールの法則 と呼ばれています。

$$\begin{align} & \nabla \cdot \bm{B} = 0\\ & \nabla \times \bm{B} = \mu_0 \bm{i}(\bm{r}) \end{align}$$

こちらも、なぜ先程の式と等価になるかの説明は省きますが、それぞれの式のイメージは以下の通りです。

• $(3)$ ガウスの法則：ここでは、磁場は発散がないことを表します。言い換えれば、磁場を発するような磁荷が存在しないこと を表します。
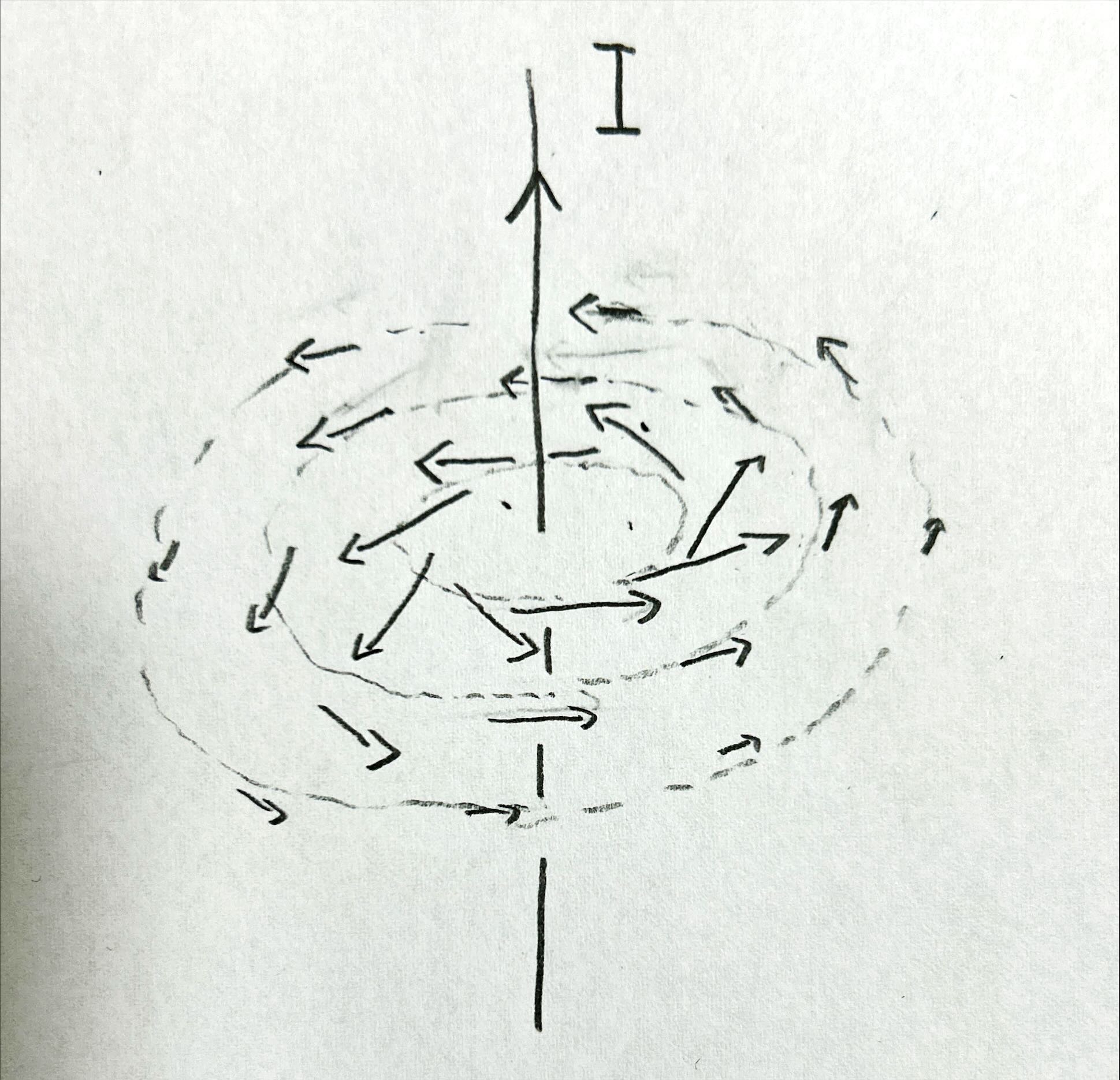
• $(4)$ アンペールの法則：電流の値に応じて、どのように磁場が渦状に広がっているかを表します。

これらの式を合わせれば、「磁場は電流の大きさに応じて、電流を中心に渦状に広がってるよね」 ということを表せるというわけです。

---

ここまで、時間変化がない場合 の、電荷と電場、電流と磁場 についてその関係性を整理しました。まとめておきましょう。

最後に 時間変化のある場合 の関係性を整理して、マクスウェルの方程式を完成させます。 数式は多いですが、頑張っていきましょう。

---

時間変化がある場合

関係性を書き直すために、実験事実による二つの法則を導入します。この二つは、時間変化がある場合 にも成り立つ法則です。

1. 電荷保存則：電子の合計は変化しない。
2. レンツの法則：磁場の変化によって、磁場の変化を抑制するような電流が生じる。

それぞれについて説明していきましょう。

---

1. 電荷保存則

電荷保存則は、電子の合計化は変化しない という法則です。

突然電子は湧いたり無くなったりすることがないというので、直感的にも理解しやすいと思います。

これを数式で表すと、以下のようになります。

これまた難しい数式ですが、イメージは以下の通りです。

• $\displaystyle \frac{\partial \rho(\bm{r})}{\partial t}$：ある位置 $\bm{r}$ における "電荷" が時間経過でどれだけ増えるか
• $\nabla \cdot \bm{i}(\bm{r})$：ある位置 $\bm{r}$ における 電流の発散がどれだけあるか

つまり、ある位置において 電流として出ていった分 $\displaystyle \left( = \nabla \cdot \bm{i}(\bm{r})\right)$ だけ、 電荷が減る $\displaystyle \left( = -\frac{\partial \rho(\bm{r})}{\partial t}\right)$というわけです。 （逆に、電流が流れ込むなら、その分の電荷が増えます。）

そうでないと、急に電子が増えたり減ったりすることになってしまいます。

アンペール・マクスウェルの法則

そして、この式を先程整理した式のうち、アンペールの法則 に組み込みましょう。

アンペールの法則は、$\nabla \times \bm{B} = \mu_0 \bm{i}(\bm{r})$ でした。 これに、電荷保存則を組み込んで拡張すると、以下のようになり、アンペール・マクスウェルの法則 と呼ばれます。

これまた数式の導出は省きますが、新たに、$\mu_0 \varepsilon_0 \frac{\partial \bm{E}(\bm{r})}{\partial t}$ という項が追加されています。 これは、端的にいうと、電場が時間変化すると、磁場が生じる ということを表しています。

つまり、電流 だけでなく 電場 も、磁場が生じる原因になるということです。

• 電荷保存則には「電荷」と「電流」しか登場しないのに、アンペール・マクスウェルの法則に「電場」が登場するのは不思議かもしれません。 しかしこれは、途中の式変形で、電場のガウスの法則 $\nabla \cdot \bm{E} = \frac{\rho(\bm{r})}{\varepsilon_0}$ を使っているためです。

---

2. レンツの法則

次に、レンツの法則について説明します。

レンツの法則は、磁場の変化によって、磁場の変化を抑制するような電流が生じる という法則です。

例えば、ある円形のコイルを通過する磁場が増加すると、その増加を抑制するような電流がコイルに生じます。図のようなイメージです。 （図はこちらより引用）

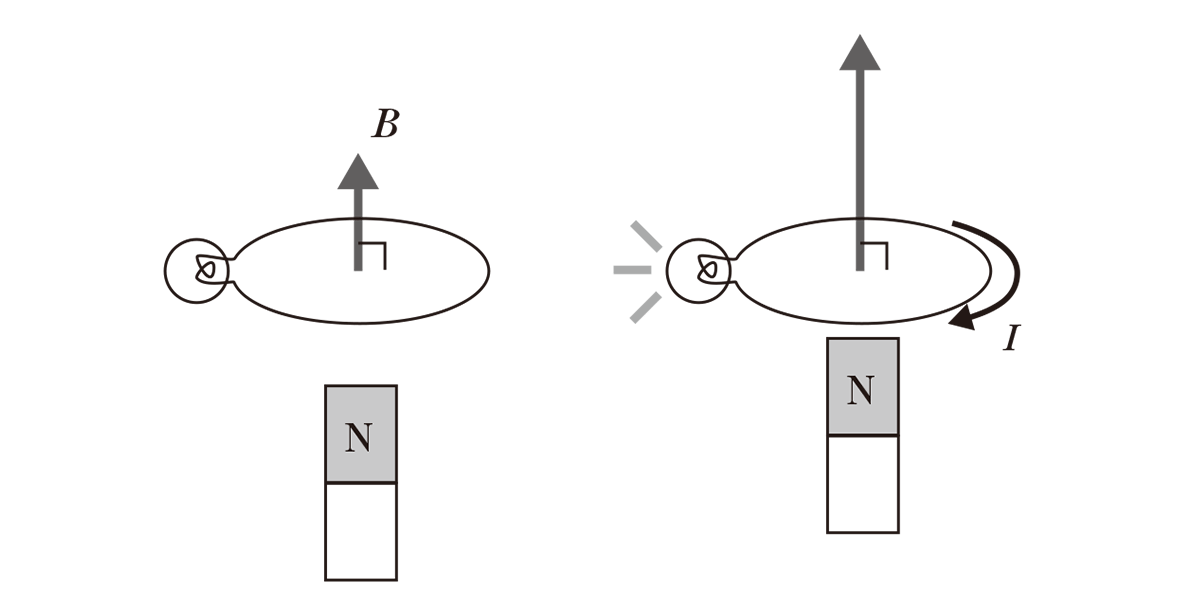
• 磁場が増加したことにより、電流が生じています。これが、レンツの法則 です。
• さらに、この電流は、ビオ・サバールの法則（もしくは アンペールの法則）によって、下向きの磁場を作り、磁場の増加を抑制する働きをします。

ファラデーの電磁誘導の法則

そして、この法則を数式で整理すると、以下のようになり、ファラデーの電磁誘導の法則 と呼ばれます。

これまた、数式の導出は省きますが、電場の回転が 0 であるという $\nabla \times \bm{E} = \bm{0}$ という式を拡張したものとなっています。

イメージとして、確かに、磁場が増加する $\displaystyle\left( = \frac{\partial \bm{B}(\bm{r})}{\partial t} > 0 \right)$ とき、 磁場を抑制する方向（つまり時計回り）の電流を生む電場が生じる $\displaystyle\left( = \nabla \times \bm{E}(\bm{r}) < 0 \right)$ ことがわかります。

• レンツの法則では「電流」と「磁場」しか登場しませんが、ファラデーの電磁誘導の法則には「電場」が登場します。 これは、厳密には、「磁場」によって「電流」が発生するのではなく、「磁場」によって「電場」が発生して「電位差」が生じることで「電流」が流れるためです。 しかし、「電位」を説明していないため、ここでは省略して説明しています。

---

ここまで、お疲れ様でした。それでは、時間変化がある場合 の関係性を整理しましょう。

これでようやく、時間変化がある場合 の電磁気学の関係性を整理できました。

それでは、最後に、これらの関係性をまとめて、マクスウェルの方程式 を完成させましょう。 といっても、マクスウェルの方程式は、先程の関係性をまとめるだけです。

---

マクスウェルの方程式

これが、電磁気学における基礎方程式となっている マクスウェルの方程式 です。

といっても、これまでの関係性を整理しただけなのに、なぜわざわざ名前をつけているの？と思うかもしれません。

しかしこれは、厳密にはこれらの関係性は 「導出」 できているわけではないため、 マクスウェル方程式を出発点として、電磁気学の理論を構築する ことを目指すのが、電磁気学のスタンダードとなっているためです。

つまり、この方程式は正しいものとして受け入れて、それ以外の現象すべては、この方程式を元にして説明しようとするのが、電磁気学の考え方です。

もう少し言い換えると、 「電荷」「電場」「電流」「磁場」をマクスウェルの方程式を満たすものとして定義して、そこから電磁気学の理論は構築される というように言えます。

---

ともあれ、これにて、電磁気学を構築する基礎方程式である、マクスウェルの方程式が完成しました。

複雑な数式が多く、わからない所も多いかもしれませんが、 マクスウェルの方程式は、電気的・磁気的な現象 を説明するための「電荷」、「電場」、「電流」、「磁場」の関係性を数式で表現したもので、電磁気学の出発となる方程式である ということだけでも覚えてもらえると良いのかな、と思います。

今回の記事はここで終わりとしますが、今回のマクスウェルの方程式は、実は、真空中の場合 に成り立つ式となっています。 物質中では、さらに複雑な方程式が必要となるのですが、それはまた別の機会に説明しましょう。（といっても、今回ほどは難しくありません）