今いる場所と同じ気温の場所は必ず無数にある!?
問題
ある２点以下の地点を除く任意の地球上の地点について、その地点の気温と全く同じ気温を持つ地点が、地球上に無数に存在することを示せ。
例えば、私が今「東京都渋谷区宇田川町３１−２のある一点」にいて、その気温が 20.1419……℃ であるとします。
すると、20.1419……℃ と無限に続いたとしても、必ずその気温と全く同じ地点が地球上に無数に存在するというのが問題文の意味です。
にわかには信じ難いですが、本当なのでしょうか。
解答
まず、地球の表面上で、その地点を通って一周する曲線を考えてみます。下図のようなイメージです。
この時の 曲線上の地点の温度変化 を考えてみましょう。例えば、図２のようになるはずです。
ここで、横軸は曲線上の地点を表し、縦軸が温度を表します。
曲線は一周しているので、グラフの左端と右端は同じ地点であり、温度も等しいはずです。
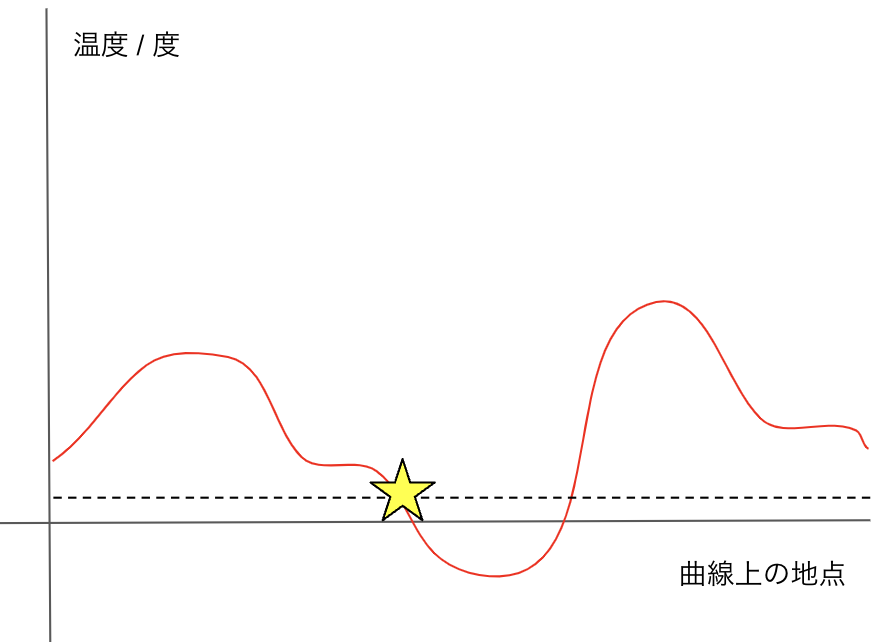
この時、このグラフではもう 1 点、星の地点と全く同じ気温となる地点があることが分かります。
また、星の地点を動かしたとしても、最大値と最小値を取る地点以外では全く同じ気温をとる地点が１点以上あることがわかります。 これは、「グラフの左端と右端は同じ地点であり、温度も等しい」という事実を使ったものです。
このことから、曲線上の最大値または最小値を取らなければ、「曲線上にその地点と全く同じ気温をとる地点が存在すること」 が示されました。
そして、ある地点を通る曲線というのは図３のように無数にとれるはずです。
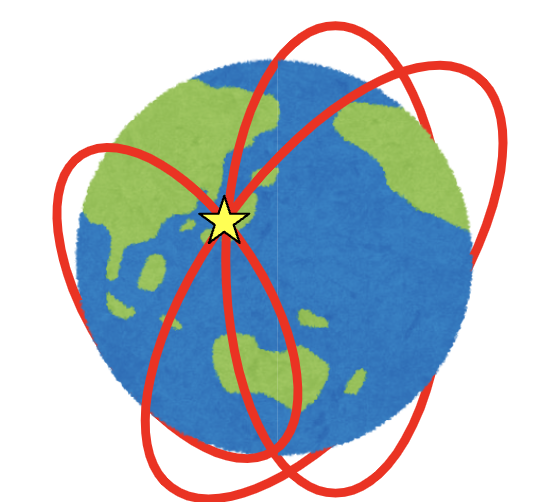
ここまでの事実をまとめると、
- その地点を通って一周する曲線上に全く同じ気温をとる地点が 1 点以上ある
- そのような曲線は無数にとれる
この二つの事実をもって、「その地点の気温と全く同じ気温を持つ地点が、地球上に無数に存在すること」 が示されています。
なお、ある曲線上では最小値か最大値になってしまう場合についても、地球上で気温が最小値 / 最大値でない場合は、 その地点が最小値 / 最大値とならない曲線を無数に取れることが簡単に示せます。 ぜひ、自分で考えてみてください。
逆に、地球上で気温が最小値 / 最大値を取る場合は、同じ気温をとる地点が存在しない可能性があります。
つまり、問題文中にある「ある２点以下の地点」というのは、地球上の気温の最小地点と最大地点というわけです。
まとめ
今回、注目したことを数学的にいうと、「連続性」 になります。
高校まででは、さわり程度しか習いませんが、数学だけでなく物理などにおいてもとても重要な概念です。
気になった方は詳しく調べてみるといいかもしれません。
注意：微視的に見ると温度が無限小数であるってどういう状況？ という話になるので、物理的に厳密な議論ではないです。 任意の地球上の地点について，ある実数で表される気温という物理量が存在すると仮定しています。
